In this post, we will see how to test a Private method in C#, using Reflection.
In unit testing, the conventional wisdom is to test the public interface of a class. This means that private methods, which are implementation details, are typically tested indirectly through public methods. However, there are times when we might want to test private methods directly, especially if they contain complex logic. While not a common practice, it’s possible to do this in C# using Reflection.
Reflection is a powerful feature in .NET that allows runtime inspection of assemblies, types, and members, and dynamic invocation of methods. This capability can be leveraged to access and test private methods in our classes.
Let’s see an example to understand how to test a private method.
First of all, we create a class Calc where we add a public method called Subtraction and a private method called IsVal1GreaterThanVal2:
[CALC.CS]
// Declare the Calc class which will contain our mathematical operations.
public class Calc
{
// Public method Subtraction that takes two integer parameters.
// This method calculates the absolute difference between two values.
public int Subtraction(int val1, int val2)
{
// Check if val1 is greater than val2 using a private method.
// This condition helps to decide the order of subtraction
// to always return a positive result.
if(IsVal1GreaterThanVal2(val1, val2))
// If val1 is greater, subtract val2 from val1.
return val1 - val2;
// If val2 is greater, subtract val1 from val2.
return val2 - val1;
}
// Private method IsVal1GreaterThanVal2 that takes two integer parameters.
// The purpose of this method is to compare two integers and return a boolean value.
// This method is an implementation detail, hidden from outside the class.
private bool IsVal1GreaterThanVal2(int val1, int val2)
{
// Check if val1 is greater than val2 and return true if so.
if (val1>val2)
return true;
// Otherwise, return false.
return false;
}
}
Then, we create a class TestCalc where we add two methods to test the Subtraction and the IsVal1GreaterThanVal2 methods:
[TESTCALC.CS]
using System.Reflection;
using TestPrivateMethod;
namespace Test
{
// This class contains unit tests for the Calc class.
public class TestCalc
{
[Fact]
public void Run_Subtraction_ShouldGiveTheSubtractionOfTwoNumber()
{
// Arrange
// Here, an instance of Calc is created to test its Subtraction method.
Calc objCal = new Calc();
// Act
// Here, the Subtraction method of objCal is called with 9 and 3 as arguments.
int result = objCal.Subtraction(9, 3);
// Assert
// Here, it's asserted that the result of the subtraction is equal to 6.
Assert.Equal(6, result);
}
[Theory]
[InlineData(9, 3, true)] // Providing test data where val1 is greater than val2.
[InlineData(3, 9, false)] // Providing test data where val1 is less than val2.
public void IsVal1GreaterThanVal2_ShouldCorrectlyEvaluate(int val1, int val2, bool expected)
{
// Arrange: Similar to above, prepare the Calc instance.
Calc calc = new Calc();
// Use reflection to access the private method IsVal1GreaterThanVal2 of the Calc class.
MethodInfo isVal1GreaterThanVal2Method = typeof(Calc).GetMethod("IsVal1GreaterThanVal2", BindingFlags.NonPublic | BindingFlags.Instance);
// Act: Invoke the private method directly using reflection, passing in test data.
bool result = (bool)isVal1GreaterThanVal2Method.Invoke(calc, new object[] { val1, val2 });
// Assert: Verify the result of the invocation matches the expected boolean value.
Assert.Equal(expected, result);
}
}
}
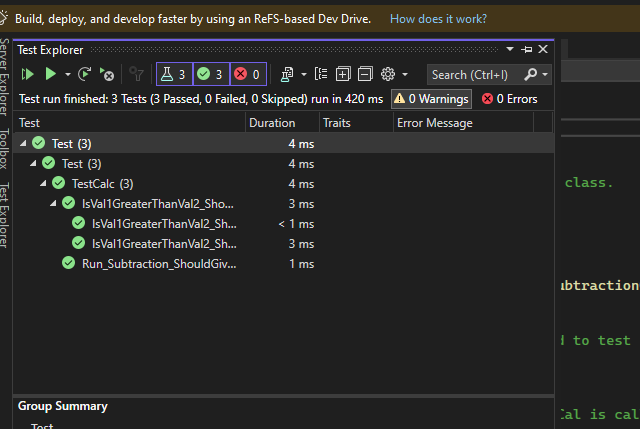
We have done and now, if we run all the test, the following will be the result: