In this post, we will see what NumPy is and how we can use it in our Python projects.
NumPy is an open-source Python library that provides support for large, multi-dimensional arrays and matrices, along with a vast collection of high-level mathematical functions to operate on these arrays efficiently. It is the foundational package for scientific computing in Python and is a key component of the data science stack.
Three important reasons to use NumPy are:
Performance: NumPy is written in C, making array operations significantly faster compared to standard Python lists.
Memory Efficiency: NumPy arrays consume less memory than equivalent Python lists.
Functionality: It offers a plethora of built-in functions for mathematical operations, statistical computations, linear algebra, random number generation, and more.
Let’s see how to use it but, first of all, we have to remember to install NumPy in our system with the command:
pip install numpy
HOW TO MANAGE AN ARRAY
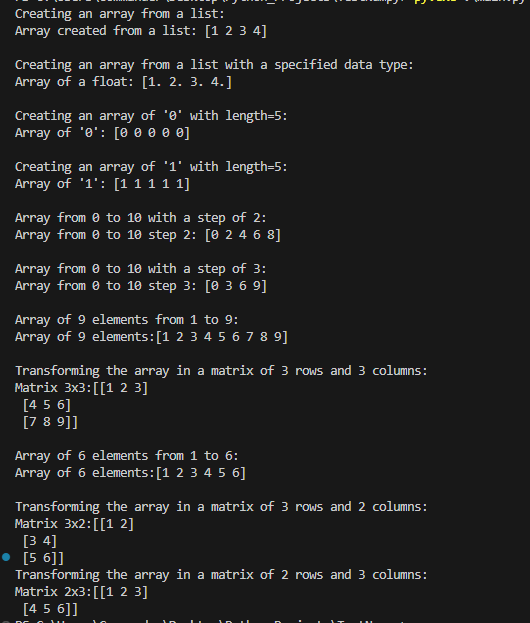
import numpy as np
# Creating an array from a list
print("Creating an array from a list:")
list1 = np.array([1, 2, 3, 4])
print(f"Array created from a list: {list1}\n")
# Creating an array from a list with a specified data type
print("Creating an array from a list with a specified data type:")
list2 = np.array([1, 2, 3, 4], dtype=float)
print(f"Array of a float: {list2}\n")
# Creating an array of '0' with length=5
print("Creating an array of '0' with length=5:")
list3 = np.zeros(5, dtype=int)
print(f"Array of '0': {list3}\n")
# Creating an array of '1' with length=5
print("Creating an array of '1' with length=5:")
list4 = np.ones(5, dtype=int)
print(f"Array of '1': {list4}\n")
# Array with a range of numbers
# from 0 to 10 with a step of 2
print("Array from 0 to 10 with a step of 2:")
list5 = np.arange(0, 10, 2)
print(f"Array from 0 to 10 step 2: {list5}\n")
# from 0 to 10 with a step of 3
print("Array from 0 to 10 with a step of 3:")
list6 = np.arange(0, 10, 3)
print(f"Array from 0 to 10 step 3: {list6}\n")
# Changing the shape of an array without changing its data
# Array of 9 elements from 1 to 9
print("Array of 9 elements from 1 to 9:")
list7 = np.arange(1, 10)
print(f"Array of 9 elements:{list7}\n")
# Transforming the array in a matrix of 3 rows and 3 columns
print("Transforming the array in a matrix of 3 rows and 3 columns:")
reshaped_list7 = list7.reshape(3, 3)
print(f"Matrix 3x3:{reshaped_list7}\n")
# Array of 6 elements from 1 to 6
print("Array of 6 elements from 1 to 6:")
list8 = np.arange(1, 7)
print(f"Array of 6 elements:{list8}\n")
# Transforming the array in a matrix of 3 rows and 2 columns
print("Transforming the array in a matrix of 3 rows and 2 columns:")
reshaped_list8 = list8.reshape(3, 2)
print(f"Matrix 3x2:{reshaped_list8}")
# Transforming the array in a matrix of 2 rows and 3 columns
print("Transforming the array in a matrix of 2 rows and 3 columns:")
reshaped_list9 = list8.reshape(2, 3)
print(f"Matrix 2x3:{reshaped_list9}")
HOW TO MANAGE A MATRIX
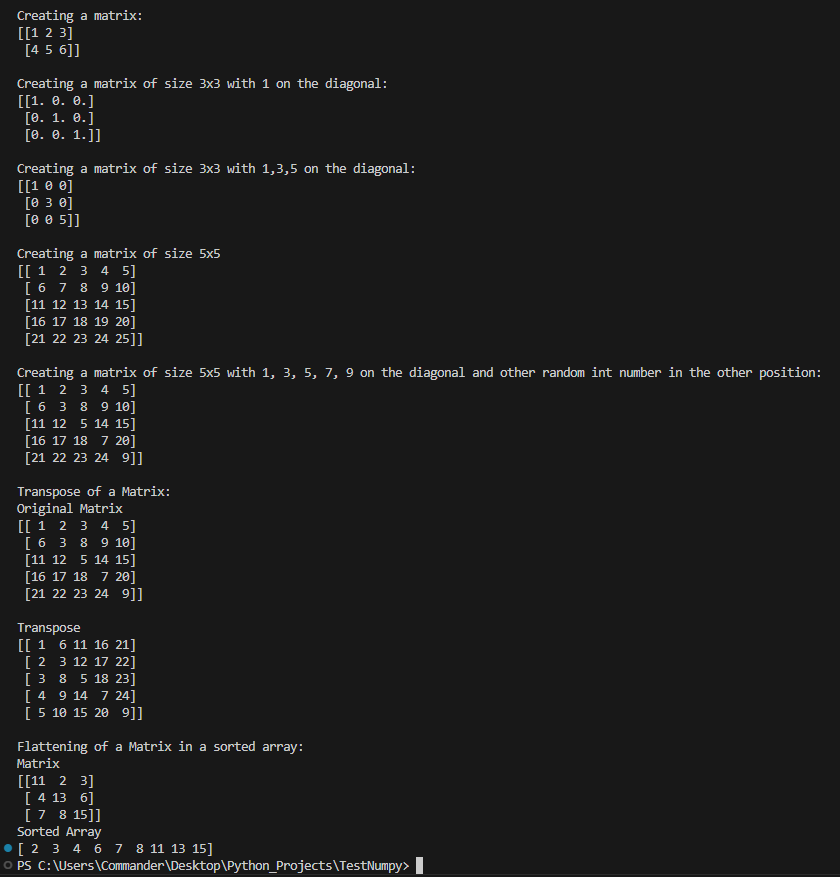
import numpy as np
# Creating a matrix
print("Creating a matrix:")
matrix = np.array([[1, 2, 3],
[4, 5, 6]])
print(f"{matrix} \n")
# Creating a matrix of size 3x3 with 1 on the diagonal
print("Creating a matrix of size 3x3 with 1 on the diagonal:")
matrix2 = np.eye(3)
print(f"{matrix2} \n")
# Creating a matrix of size 3x3 with 1,3,5 on the diagonal
print("Creating a matrix of size 3x3 with 1,3,5 on the diagonal:")
matrix3 = np.diag([1, 3, 5])
print(f"{matrix3} \n")
# Creating a matrix of size 5x5
print("Creating a matrix of size 5x5")
matrix4 = np.arange(1, 26).reshape(5, 5)
print(f"{matrix4} \n")
# Creating a matrix of size 5x5 with 1,3,5,7,9 on the diagonal and other
# random int number in the other position
print("Creating a matrix of size 5x5 with 1, 3, 5, 7, 9 on the diagonal and other random int number in the other position:")
# create an array and then reshape it in a matrix 5x5
matrix5 = np.arange(1, 26).reshape(5, 5)
# set the diagonal with the number 1,3,5,7,9
np.fill_diagonal(matrix5, [1, 3, 5, 7, 9])
print(f"{matrix5} \n")
# Transpose of a Matrix
print("Transpose of a Matrix:")
print("Original Matrix")
print(f"{matrix5} \n")
print("Transpose")
print(f"{matrix5.T} \n")
# Flattening of a Matrix
print("Flattening of a Matrix in a sorted array:")
print("Matrix")
matrix6 = np.arange(1, 10).reshape(3, 3)
# set the diagonal with the number 11,13,15
np.fill_diagonal(matrix6, [11, 13, 15])
print(matrix6)
# Flatten the matrix6 into an array (flatten()) and sort it in ascending order
new_array = np.sort(matrix6.flatten())
print("Sorted Array")
print(new_array)
OPERATIONS
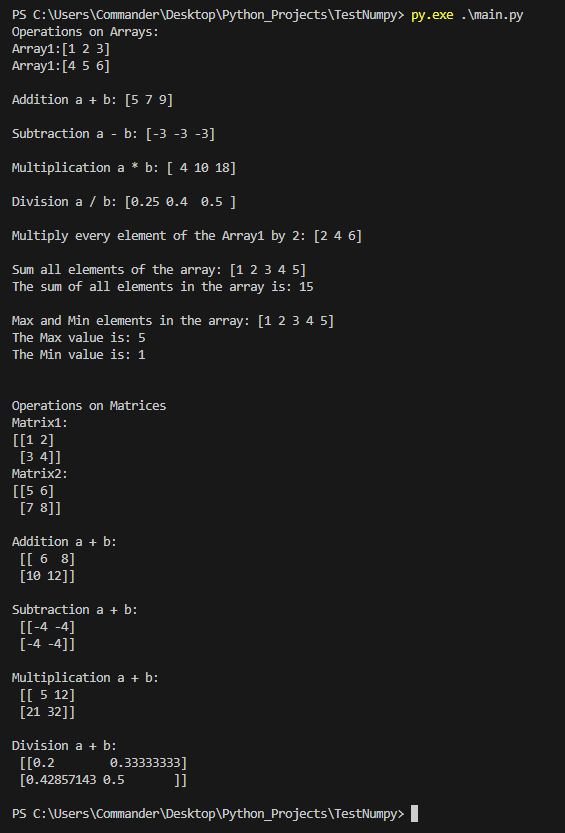
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print("Operations on Arrays:")
print(f"Array1:{a}")
print(f"Array1:{b} \n")
# Addition
print(f"Addition a + b: {a+b} \n") # Output: [5 7 9]
# Subtraction
print(f"Subtraction a - b: {a - b} \n") # Output: [-3 -3 -3]
# Multiplication
print(f"Multiplication a * b: {a * b} \n") # Output: [ 4 10 18]
# Division
print(f"Division a / b: {a / b} \n") # Output: [0.25 0.4 0.5 ]
# Multiply every element by 2
# Output: [2 4 6]
print(f"Multiply every element of the Array1 by 2: {a * 2} \n")
# Sum all elements of an array
arr = np.array([1, 2, 3, 4, 5])
print(f"Sum all elements of the array: {arr}")
print(f"The sum of all elements in the array is: {np.sum(arr)} \n")
# Max an Min elements in an array
print(f"Max and Min elements in the array: {arr}")
print(f"The Max value is: {np.max(arr)}")
print(f"The Min value is: {np.min(arr)} \n\n")
# Operations on Matrices
print(f"Operations on Matrices")
matrix1 = np.array([[1, 2],
[3, 4]])
matrix2 = np.array([[5, 6],
[7, 8]])
print(f"Matrix1:")
print(matrix1)
print(f"Matrix2:")
print(f"{matrix2} \n")
print(f"Addition a + b: \n {matrix1 + matrix2} \n")
print(f"Subtraction a + b: \n {matrix1 - matrix2} \n")
print(f"Multiplication a + b: \n {matrix1 * matrix2} \n")
print(f"Division a + b: \n {matrix1 / matrix2} \n")
MANAGING INDEXING
import numpy as np
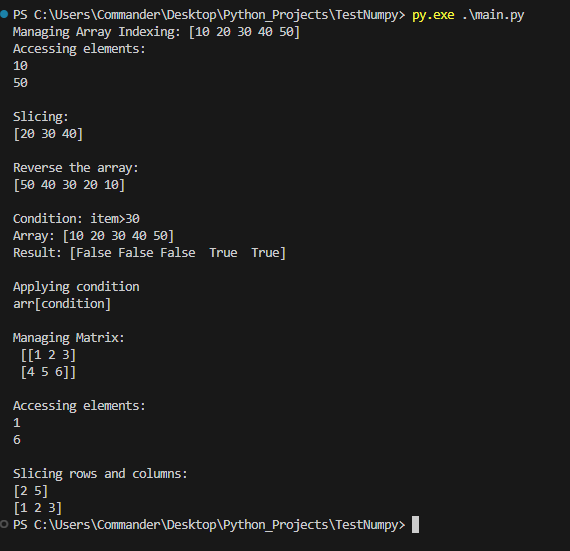
arr = np.array([10, 20, 30, 40, 50])
print(f"Managing Array Indexing: {arr}")
# Accessing elements
print("Accessing elements:")
print(arr[0]) # Output: 10
print(f"{arr[-1]} \n") # Output: 50
# Slicing
print("Slicing:")
print(f"{arr[1:4]} \n") # Output: [20 30 40]
# Reverse the array
print("Reverse the array:")
print(f"{arr[::-1]} \n") # Output: [50 40 30 20 10]
# Condition
print("Condition: item>30")
condition = arr > 30
print(f"Array: {arr}")
print(f"Result: {condition} \n") # Output: [False False False True True]
# Applying condition
print("Applying condition")
print(f"arr[condition] \n") # Output: [40 50]
matrix = np.array([[1, 2, 3],
[4, 5, 6]])
print(f"Managing Matrix: \n {matrix} \n")
# Accessing elements
print("Accessing elements:")
print(matrix[0, 0]) # Output: 1
print(f"{matrix[1, 2]} \n") # Output: 6
# Slicing rows and columns
print("Slicing rows and columns:")
print(matrix[:, 1]) # Output: [2 5] (Second column)
print(matrix[0, :]) # Output: [1 2 3] (First row)
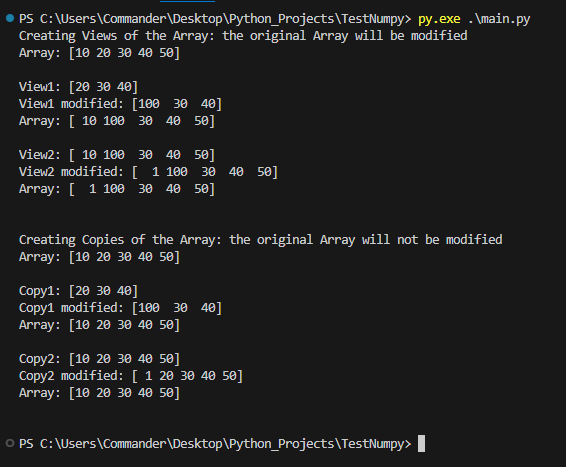
VIEWS AND COPIES
import numpy as np
arr = np.array([10, 20, 30, 40, 50])
print(f"Creating Views of the Array: the original Array will be modified")
print(f'Array: {arr} \n')
view1 = arr[1:4] # [20, 30, 40]
print(f"View1: {view1}")
view1[0] = 100
print(f"View1 modified: {view1}")
print(f'Array: {arr} \n')
view2 = arr
print(f"View2: {view2}")
view2[0] = 1
print(f"View2 modified: {view2}")
print(f'Array: {arr} \n\n')
arr2 = np.array([10, 20, 30, 40, 50])
print(f"Creating Copies of the Array: the original Array will not be modified")
print(f'Array: {arr2} \n')
copy1 = arr2[1:4].copy() # [20, 30, 40]
print(f"Copy1: {copy1}")
copy1[0] = 100
print(f"Copy1 modified: {copy1}")
print(f'Array: {arr2} \n')
copy2 = arr2.copy()
print(f"Copy2: {copy2}")
copy2[0] = 1
print(f"Copy2 modified: {copy2}")
print(f'Array: {arr2} \n\n')